为什么要研究算法,算法到底有什么用?

看这道题:
已知 a+b+c=1000 且a^2+b^2=c^2 求 a、b、c 有可能出现的组合。
一般我们看到这道题,就是for循环吧
这样写:
for($a=1;$a<=1000;$a++){
for($b=1;$b<=1000;$b++){
for($c=1;$c<=1000;$c++){
if($a+$b+$c===1000 && bcpow($a,2)+bcpow($b,2)==bcpow($c,2)){
printf("a b c %d,%d,%d \n",$a,$b,$c);
}
}
}
}
//三层循环嵌套,谁知道这要运行多少次的计算
1000*1000*1000=?
#结果:
#a+b+c=1000,且a^2+b^2=c^2 问 a b c 可能的值是:
#a b c 200,375,425
#a b c 375,200,425
#[Finished in 78.4s]
#-----------------------------------------------------
那么有没有改良的程序:
#设 a^2+b^2=c^2
#则 a、b、b至少等于1 ,因此 减去 3
#只需要循环到997
printf("\n\na+b+c=1000,且a^2+b^2=c^2 问 a b c 可能的值是:\n");
$sum=1000;
for($a=1,$num=$sum-3;$a<=$num;$a++){
for($b=1;$b<$num-$a;$b++){
$c=$sum-$a-$b;
if($a+$b+$c===1000 && bcpow($a,2)+bcpow($b,2)==bcpow($c,2)){
printf("a b c %d,%d,%d \n",$a,$b,$c);
}
}
}
#a+b+c=1000,且a^2+b^2=c^2 问 a b c 可能的值是:
#a b c 200,375,425
#a b c 375,200,425
#[Finished in 1.6s]这就是算法的魅力,就这么一个循环就能看出一个程序员水平的高低。
一个执行了 78.4s 一个1.6s 这差出多少倍?
先看一道数学题吧,
1+3+5+7+9+...+100 问得多少? 从1到100的奇数相加是多少
1+2+3+4+5+6+7+...100 得多少?从1到100相加之和是多少?
2+4+6+8+...100 得多少? 从1到100的偶数相加?
当我们看到这样的题之后,最先想到的是 写一个函数,循环从1到100 相加最后返回结果
这没有错误,符合程序的规则。
那来看看如何写这个函数:
function sum($start,$end){
$sum=0;
for($i=$start,$i<=$end;$i++){
$sum+=$j;
}
return $sum;
}
echo sum(1,100); //5050看到上面的函数和执行结果,我们写完了,那是不是最佳的方式方法呢?
显然不是,我们利用数学公式看看
(1+100)*100/2 如果使用这个公式,程序运行一遍,即可得到结果。既然有这样的算法,为什么要从1到100 循环呢?
//这是我们优化后的一种写法
function sum($start,$end){
return ($start+$end)*$end/2;
}这种写法,就得说说算法了。
算法是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,
算法代表着用系统的方法描述解决问题的策略机制。
也就是说,能够对一定规范的输入,在有限时间内获得所要求的输出。
其实编程限制了我们的想法,只要for循环就可以了。没有想起我们学习的数学公式。
为什么要使用算法呢?
就是为了一类问题,使用快速而优的方法得到想要的答案。
同样我们看看:我们看看1到100奇数加起来是多少
//需要执行50次 ceil(100/2) //如果遇到余数,总是向上进1
for ($j = 1, $num = 0, $sum = 0; $j <= 100; $j = $j + 2) {
//printf("%s\n", $j);
$num++;
$sum += $j;
}
printf("1+3+5+7+9+....+100结果是:%s\n", $sum);
// 这就是算法的精髓,根据题的规律,一次执行行到结果
function jiaddSum($start, $end) {
$diff = 0;
if ($start > 1) {
$diff = floor($start / 2);
}
bcmod($end, 2) == 0 && $end--;
$num = ceil($end / 2);
return ($start + $end) * ($num - $diff) / 2;
}
echo "\n";
echo jiaddSum(1, 100);总上所述,如果不研究算法,程序会使用for循环计算很多次,时间、内存都有所消耗。
如果使用使用我们的算法,那么就会快很多,
从1到100之间的奇数计算,使用for 循环 需要计算 50次
使用计算公式: 一次执行,通过几次数学公式 就能快速计算出结果。
通过这里,得到了些什么呢?
计算机部分编程与课本中的一些公式是息息相关的,可以借鉴数学公式、数学定论 得到结果。
计算机常见的几种算法:
冒泡排序
插入排序
选择排序
快速排序
二分查找
顺序查找
冒泡排序
/**
* 冒泡排序
* @param [type] $arr [description]
* @return [type] [description]
*/
function arrSort($arr) {
for ($i = 1, $len = count($arr); $i < $len; $i++) {
for ($j = 0; $j < $len - $i; $j++) {
if ($arr[$j] > $arr[$j + 1]) {
$temp = $arr[$j];
$arr[$j] = $arr[$j + 1];
$arr[$j + 1] = $temp;
}
}
}
return $arr;
}
//冒泡排序法的改良版
//如果这是一个有序的列表,那么放在这个方法执行中,会很快的返回
//时间复杂度 O(n)
function arrSrot2($data){
$len=count($data);
if($len<=1)
return $data;
$change=false;
for($i=1;$i<$len;$i++){
for($j=0;$j<$len-$i;$j++){
//判断,如果前边的一个值 大于后边的值,则进行交换
if($data[$j]>$data[$j+1]){
$temp=$data[$j+1];
$data[$j+1]=$data[$j];
$data[$j]=$temp;
$change=true;
}
}
if($change==false)
break;
}
return $data;
}例如数组:
$arr = array(10, 2, 36, 14, 25, 23, 85, 99, 45);
数组中共计9个数, 会执行多少次排序完毕?
先看看循环的轮数 for($i=1;$i<count($arr);$i++) 也就是8轮 公式: $len-1 =8 等同于 9-1
8轮循环完毕
再看里面的循环:
当 $i=1 ,=2,=3分别里面会循环几次
$i=1 ,$j从0 开始 循环到 9-$i =8 走了 8次
$i=2 ,$j从0 开始 循环到 9-$i =7 走了 7次
$i=3 ,$j从0 开始 循环到 9-$i =6 走了 6次
$i=4 ,$j从0 开始 循环到 9-$i =5 走了 5次
$i=5 ,$j从0 开始 循环到 9-$i =4 走了 4次
$i=6 ,$j从0 开始 循环到 9-$i =3 走了 3次
$i=7 ,$j从0 开始 循环到 9-$i =2 走了 2次
$i=8 ,$j从0 开始 循环到 9-$i =1 走了 1次
当等于9的时候,for不成立,退出。
因此 走了8轮。
则:8+7+6+5+4+3+2+1=36 使用数学公式计算 (8+1)*8/2=36
因此冒泡排序法最少排序=
冒泡排序法循环次数:$len*($len-1)/2
$len=数组的长度
$arr = array(10, 2, 36, 14, 25, 23, 85, 99, 45, 88, 33, 26, 57, 56, 72); 15个数 15*(15-1)/2=105
$arr = array(10, 2, 36); 3个数 3*(3-1)/2=3
$arr = array(10, 2, 36, 14, 25); 5个数 5*(5-1)/2=10
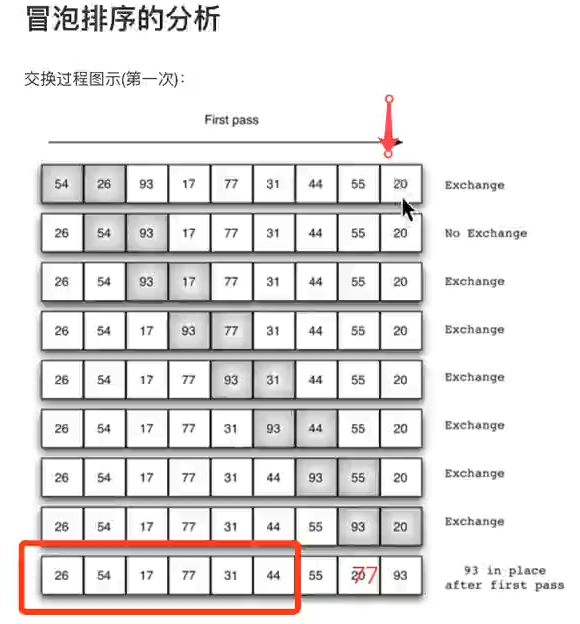
结论:就是把相邻的两个数值比较,把最大值向后移动。
轮数: for $i=1 从1开始
$j=0;$j<$len-$i;$j++
这是核心。
时间复杂度:
最坏时间复杂度:O(n2)
最优时间复杂度:O(n)
稳定程度:稳定
插入排序
操作的是前半部分
function insertSort($arr){
for($i=1;$i<count($arr);$i++){
$j=$i; //内层循环 起始
while($j>0 && $arr[$j]<$arr[$j-1]){
$temp=$arr[$j-1];
$arr[$j-1]=$arr[$j];
$arr[$j]=$temp;
$j--;
}
}
return $arr;
}
$result=insertSort($arr);
print_r($result);从后往前 去比较 ,比较过程中,如果前边一个值小于后天这个值,则跳出循环
while($j>0 && $arrr[$j]<$arr[$j-1]){
//只有j>0 且 $j < $j-1 才执行数据交换。
}
我们数据交换的时候,使用list() 这个方式进行交换,效率会怎么样????
时间复杂度:
最坏时间复杂度:O(n2)
最优时间复杂度:O(n)
稳定程度:稳定
选择排序
简单直观的排序算法, 从里面找最小的值,找到后,循环,替换
重点考虑后边顺序,
默认取出第一个值为最小值, 循环
$min=$i
再一次循环,这次循环比较特殊
function selectSort($data){
$len=count($data);
for($i=0;$i<$len-1;$i++){
$min=$i;
for($j=$i+1;$j<$len;$j++){
if($data[$min]>$data[$j]){
$min=$j;
}
}
$temp=$data[$min];
$data[$min]=$data[$i];
$data[$i]=$temp;
}
return $data;
}
print_r($sresult);时间复杂度:O(n2)
稳定程度:不稳定
希尔排序
function shell_sort($data){
$len=count($data);
$gap=floor($len/2);
while($gap>0){
for($i=$gap;$i<$len;$i++){
$j=$i;
while($j>0 && $data[$j-$gap]>$data[$j]){
$temp=$data[$j];
$data[$j]=$data[$j-$gap];
$data[$j-$gap]=$temp;
$j-=$gap;
}
}
$gap=floor($gap/2);
}
return $data;
}
$arr = array(10, 2, 36, 14, 25, 23, 85, 99, 45);
printf("希尔排序法:\n%s\n",var_export(shell_sort($arr),true));结果展示:
希尔排序法: array ( 0 => 2, 1 => 10, 2 => 14, 3 => 23, 4 => 25, 5 => 36, 6 => 45, 7 => 85, 8 => 99, )
快速排序
/**
* 快速排序法
*
* @desc 注意事项:for 循环开始的$key 是1
* @param [type] $arr [description]
* @return [type] [description]
*/
function quickSort($arr) {
static $quickSortNum = 0;
static $lun = 0;
printf("\n\n\n-----------轮数:%d\n", ++$lun);
if (count($arr) <= 1) {
return $arr;
}
$firstVal = $arr[0];
$leftArr = [];
$rightArr = [];
for ($i = 1; $i < count($arr); $i++) {
if ($arr[$i] < $firstVal) {
$leftArr[] = $arr[$i];
} else {
$rightArr[] = $arr[$i];
}
printf("\nquickSort执行的次数:%d >>>>数组:%s", ++$quickSortNum, var_export($arr, true));
}
$leftArr = quickSort($leftArr);
$rightArr = quickSort($rightArr);
return array_merge($leftArr, [$firstVal], $rightArr);
}19次就排序完毕
二分查找
function erfen($arr, $val, $min = 0, $big = null) {
static $num = 0;
is_null($big) && $big = count($arr);
if ($big < $min) {
return -1; //如果找不到数据就返回-1
}
//$middle = intval(($min + $big) / 2);
$middle=bcdiv(bcadd($min,$big),2);
printf("查找%d位置的次数:%d\n", $val, ++$num);
//echo $arr[$middle];
if ($arr[$middle] == $val) {
return $middle;
} else if ($arr[$middle] < $val) {
return erfen($arr, $val, $middle + 1, $big);
} else if ($arr[$middle] > $val) {
return erfen($arr, $val, $min, $middle - 1);
}
}
echo erfen($v, 36);
/**
Array
(
[0] => 2
[1] => 10
[2] => 14
[3] => 23
[4] => 25
[5] => 36
[6] => 45
[7] => 85
[8] => 99
)
**/二分查找:前提必须是 有序数组
查询结果:
查找36位置的次数:1
查找36位置的次数:2
查找36位置的次数:3
可以看出 共计循环了3次
位置是:
5
如果不使用二分查找,则使用 foreach 查找法,则循环的是 6 次
顺序查找
function shunxuSort($arr,$findVal){
$result=-1;
foreach($arr as $key=>$val){
if($val==$findVal){
$result=$key;
break;
}
}
return $result;
}2018-11-2练习题
<?php
$arr = array(10, 2, 36, 14, 25, 23, 85, 99, 45);
function quickSort($arr){
$count=count($arr);
if ($count <= 1) {
return $arr;
}
$first=$arr[0];
$left=[];
$right=[];
for($i=1;$i<$count;$i++){
$arr[$i]<$first?$left[]=$arr[$i]:$right[]=$arr[$i];
}
$left=quickSort($left);
$right=quickSort($right);
return array_merge($left,[$first],$right);
}
$newarr=quickSort($arr);
print_r($newarr);
//冒泡
function maopao($arr){
if(count($arr)==1)
return $arr;
for($i=1;$i<count($arr);$i++){
for($j=0;$j<count($arr)-$i;$j++){
if($arr[$j]>$arr[$j+1]){
$temp=$arr[$j];
$arr[$j]=$arr[$j+1];
$arr[$j+1]=$temp;
}
}
}
return $arr;
}
print_r(maopao($arr));
function erfen($arr,$val,$min=0,$big=null){
if(empty($arr)) return $arr;
is_null($big) && $big=count($arr);
if ($big < $min) {
return -1;
}
//$middle=intval(bcadd($min,$big)/2);
$middle=bcdiv(bcadd($min,$big),2);
if($arr[$middle]==$val){
return $middle;
}else if($arr[$middle]<$val){
return erfen($arr,$val,$middle+1,$big);
}else{
return erfen($arr,$val,$min,$middle-1);
}
}
$findval=45;
$newdata=maopao($arr);
printf("查找数组%s中%s的索引值是%s\n\n",var_export($newdata,true),$findval,erfen($newdata,$findval));
function insertSort($arr){
if(count($arr)<=1){
return $arr;
}
for($i=1;$i<count($arr);$i++){
$j=$i;
while($j>0 && $arr[$j]<$arr[$j-1]){
$temp=$arr[$j];
$arr[$j]=$arr[$j-1];
$arr[$j-1]=$temp;
$j--;
}
}
return $arr;
}
print_r(insertSort($arr));2018-12-3练习排序法
$arr = array(10, 2, 36, 14, 25, 23, 85, 99, 45);
//插入排序
function insertSort($data){
$len=count($data);
if($len<=1)
return $data;
for($i=1;$i<$len;$i++){
$j=$i;
while($j>0 && $data[$j-1]>$data[$j]){
$temp=$data[$j-1];
$data[$j-1]=$data[$j];
$data[$j]=$temp;
$j--;
}
}
return $data;
}
printf("原始数组展示:\n%s\n",var_export($arr,true));
printf("插入排序法:\n%s\n",var_export(insertSort($arr),true));
//选择排序
function selectSort($data){
$len=count($data);
for($i=0;$i<$len-1;$i++){
$min=$i;
for($j=$i+1;$j<$len;$j++){
if($data[$min]>$data[$j]){
$min=$j;
}
}
$temp=$data[$min];
$data[$min]=$data[$i];
$data[$i]=$temp;
}
return $data;
}
printf("选择排序法:\n%s\n",var_export(selectSort($arr),true));
//希尔排序
function shell_sort($data){
$len=count($data);
$gap=floor($len/2);
while($gap>0){
for($i=$gap;$i<$len;$i++){
$j=$i;
while($j>0 && $data[$j-$gap]>$data[$j]){
$temp=$data[$j];
$data[$j]=$data[$j-$gap];
$data[$j-$gap]=$temp;
$j-=$gap;
}
}
$gap=floor($gap/2);
}
return $data;
}
printf("希尔排序法:\n%s\n",var_export(shell_sort($arr),true));